The Archimedes principle states that any object immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid displaced by the object. This fundamental physical law, discovered by the ancient Greek mathematician Archimedes in the 3rd century BCE, explains why objects float or sink in fluids. When an object's density is less than the surrounding fluid's density, the buoyant force exceeds the object's weight, causing it to float or rise; when its density is greater, it sinks.

Archimedes discovered his famous buoyancy principle while attempting to solve a problem for King Hiero II of Syracuse who suspected a goldsmith of replacing some gold with silver in a crown. The king asked Archimedes to verify its composition without damaging it. The solution reportedly came to Archimedes while bathing, when he noticed water displacement as he entered the tub. This observation led to his celebrated "Eureka!" moment. He realized that by immersing an object in water, he could measure its volume through displacement. Since gold is denser than silver, comparing the crown's weight to its volume would reveal if it contained silver. He documented this finding in "On Floating Bodies" establishing a mathematical relationship between an object's weight, volume, and fluid properties. T

It's application to high-altitude ballooning

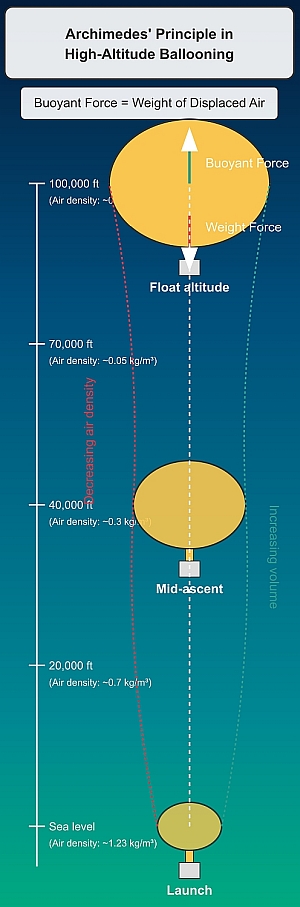
Archimedes' principle applies directly to high-altitude ballooning through the relationship between buoyant force and displaced air. The diagram at left illustrates how this principle operates across different altitudes during a balloon's ascent.

At launch near sea level, the balloon contains helium or hydrogen gas that is significantly less dense than the surrounding atmosphere (density ~1.23 kg/m3). Following Archimedes' principle, the balloon experiences an upward buoyant force equal to the weight of the displaced air. Since this buoyant force exceeds the combined weight of the balloon system (envelope, gas, and payload), the balloon rises.

As the balloon ascends, it encounters progressively less dense atmospheric layers. At 30,000 feet, the air density drops to approximately 0.46 kg/m3, and by 100,000 feet, it plummets to around 0.01 kg/m3. This dramatic decrease in ambient pressure causes the lifting gas inside the balloon to expand according to Boyle's Law (P1V1 = P2V2).

The expanding gas increases the balloon's volume, allowing it to displace more air and maintain positive buoyancy despite the decreasing air density. This is why high-altitude balloons are typically launched partially inflated-they must accommodate this substantial expansion at higher altitudes. A balloon that appears only 10-20% filled at launch might expand to full capacity as it approaches its float altitude.

The balloon continues to rise until it reaches a point of neutral buoyancy, where the buoyant force exactly equals the weight of the entire system. At this equilibrium point, the balloon stops ascending and begins to "float" at its maximum altitude. For scientific balloons, this can often be between 80,000-120,000 feet in the stratosphere.

The float altitude can be precisely calculated and controlled by adjusting the amount of lifting gas and total system weight. This relationship derives directly from Archimedes' principle: when the weight of displaced air equals the total weight of the balloon system, neutral buoyancy is achieved.

Weather changes or gas leakage can disrupt this equilibrium. If the balloon loses gas or encounters colder temperatures (causing the gas to contract), the buoyant force decreases, potentially causing descent. Conversely, solar heating during daylight hours can increase gas expansion and buoyancy, causing the balloon to rise further.

This application of Archimedes' principle, combined with the predictable behavior of gases under changing pressure conditions, allows scientists and engineers to design high-altitude balloon missions that can reach specific altitudes and remain there for extended periods, enabling atmospheric research, telecommunications, and other applications at a fraction of the cost of satellite deployment.